Dane 15-minutowe z godzinowych

 

14 czerwca 2024 r. weszła w życie reforma rynku bilansującego w Polsce. Jedną ze zmian jest wprowadzenie 15-minutowego okna rozliczeń energii w miejsce obecnego – godzinowego. Dla analityków rynku energii może to rodzić szereg wyzwań, np. jak na podstawie danych godzinowych tworzyć projekcje cen lub zapotrzebowania na energię w granulacji 15-minutowej.

Do zwiększania rozdzielczości danych (zagęszczania) może służyć wiele metod interpolacyjnych. W przypadku szeregów czasowych najlepiej nadają się do tego krzywe sklejane. Które dają najlepsze wyniki? W tym artykule sprawdziłem następujące interpolacje:

• stałą, tj. przyjęcie wartości z najbliższego węzła,
• liniową,
• kwadratową,
• sześcienną naturalną (natural cubic spline) oraz
• niektóre odmiany interpolacji sześciennej, tj. interpolację Akimy, Hermite’a (Catmulla-Roma), Kochanka-Bartelsa , Steffena oraz Steffena – miękką.

Zakres danych, metoda weryfikacji i wybór miary błędu interpolacji

Do analizy wybrałem wielkości publikowane w rozdzielczości 15-minutowej w BPKD (bieżącym planie koordynacyjnym dobowym) przez Polskie Sieci Elektroenergetyczne (#PSE) od 14 czerwca do 25 sierpnia 2024 r. Dane najpierw celowo „rozrzedziłem”, tj. zagregowałem do danych godzinowych (przyjąłem, że wartością reprezentatywną jest wartość średnią z czterech kwadransów każdej godziny i założyłem, że wartość ta obowiązuje dokładnie w 30. minucie godziny), a następnie dane te rozagregowałem na przedziały 15-minutowe, ale już przy użyciu badanych algorytmów interpolacyjnych. Wreszcie, wyniki interpolacji odniosłem do wartości wyjściowych i na tej podstawie wyznaczyłem błędy interpolacji dla każdej metody.

Jako miary błędu użyłem średniego względnego błędu prognozy MAPE (Mean Absolute Percentage Error):

MAPE = |F – A| / A

gdzie F to wartość otrzymana z algorytmu interpolacji, a A to wartość faktycznie zaobserwowana (opublikowana). Naturalnie, tak zdefiniowana miara mogła być użyta tylko dla tych wielkości, które nie przyjmują wartości zerowych lub bliskich zeru, a więc dla:

• zapotrzebowania na moc KSE,
• planowanych ograniczeń dyspozycyjności i odstawień MWE,
• sumy generacji jednostek grafikowych w KSE (JGw, JGm, JGz i JGa),
• sumy generacji jednostek grafikowych wytwórczych (JGw),
• sumarycznej generacji jednostek wytwórczych nieuczestniczących aktywnie w RB,
• sumy zdolności wytwórczych jednostek grafikowych wytwórczych (JGw1),
• sumy zdolności wytwórczych jednostek wytwórczych w KSE (JGw, JGm, JGz i JGa),
• rezerwy mocy ponad zapotrzebowanie,
• rezerwy mocy poniżej zapotrzebowania.

Tam zaś, gdzie występowały wartości zerowe, zmodyfikowałem miarę błędu w taki sposób, że jako punkt odniesienia wybrałem maksymalną wartość zaobserwowaną w badanym okresie:

MAPE = |F – A| / S

gdzie F i A mają te same znaczenia co wyżej, natomiast S oznacza właśnie wartość maksymalną zaobserwowaną w badanym okresie, odpowiednio dla poniższych wielkości:

• sumy generacji jednostek grafikowych magazynów (JGm1),
• sumy zdolności wytwórczych jednostek grafikowych magazynów (JGm1),
• sumarycznej generacji źródeł fotowoltaicznych,
• sumarycznej generacji źródeł wiatrowych,
• sumarycznej mocy ładowania JGm.

Wyniki błędów interpolacji

Krótki rzut oka na animowany rysunek poglądowy dla zapotrzebowania na moc KSE w dniu 20 czerwca 2024 r. wystarczy, by spośród rozpatrywanych algorytmów interpolacji od razu wykluczyć interpolację kwadratową. Dla porządku jednak poniżej podałem wyniki dla wszystkich metod – kolorem czerwonym oznaczyłem te najgorsze, kolorem zielonym – najlepsze:

Cena, jaką płacimy za ciągłość pochodnej, jest nieproporcjonalnie wysoka w stosunku do otrzymanych rezultatów, co ilustruje poniższy wykres dla wybranej doby:

Po usunięciu interpolacji kwadratowej z listy, najsłabsze rezultaty daje interpolacja wielkościami stałymi z najbliższego dostępnego węzła:

Nic w tym dziwnego – interpolacja stałymi jest właściwie założeniem, że w każdym kwadransie godziny mamy wartość średnią z czterech kwadransów:

Jej stosowanie jest uzasadnione tylko wtedy, gdy mamy pewność, że dane wyjściowe są faktycznie godzinowe (tak jak obecnie w przypadku krajowego salda wymiany międzysystemowej w BPKD), co oznacza, że w istocie nie potrzebujemy interpolacji.

Interpolacja liniowa, pomimo swojej prostoty, w porównaniu do interpolacji stałymi radzi sobie całkiem nieźle. Natomiast poza nielicznymi wyjątkami, jej wyniki są w przeważającej mierze gorsze od wyników interpolacji funkcjami sześciennymi:

Mimo to, warto ją rozważyć z oczywistego powodu – jest wyjątkowo prosta w implementacji.

Porównanie samych metod sześciennych przedstawia się następująco (kolory zostały przeskalowane do zaktualizowanego zakresu wartości błędów):

Tutaj wyniki nie są już tak jednoznaczne i mogą zależeć od interpolowanej wielkości. Średnio najlepiej wypadają obie metody Steffena i metoda Akimy. Dla funkcji sześciennej naturalnej wyniki są najczęściej minimalnie gorsze – prawdopodobnie na skutek niespełnienia warunku na monotoniczność funkcji interpolacji pomiędzy węzłami z powodu obowiązywania warunku na ciągłość drugiej pochodnej w punktach węzłowych.

Do wyboru optymalnej metody można użyć także np. rankingu dla każdej z badanych wielkości:

Przy tym podejściu także najlepsza okazała się metoda Steffena (miękka), dalej już nieco inaczej niż przy średniej, tj. kolejno metoda Akimy i metoda Hermite’a. Poniżej znajdują się wizualizacje rezultatów dla tych trzech algorytmów dla wybranej doby 20 czerwca – charakteryzowała się ona największym rozrzutem wyników wśród tych metod (akurat dla tej doby metoda Akimy dała minimalnie lepszy wynik niż ogólnie lepsza dla całego zakresu danych metoda Steffena – miękka):

Wracając do tabel z wartościami MAPE warto zwrócić uwagę, że wyniki interpolacji dla rezerw mocy są dużo słabsze od wyników interpolacji dla pozostałych wielkości publikowanych w ramach BPKD. Dlatego na poniższym histogramie rezerwy nie zostały pokazane, aby nie zaburzać skali dla pozostałych wielkości:

Słabsze wyniki interpolacji dla rezerw mają związek z tym, że mogą one zmieniać się w skokowy sposób z kwadransa na kwadrans. Przykładowo, dla tej samej doby 20 czerwca 2024 r. pomiędzy godzinami 18:00 a 20:00 wystąpiło kilka takich silnych wahnięć:

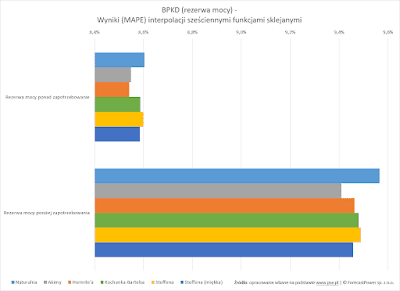
Dlatego właśnie wyniki błędów interpolacji dla obu rezerw mieszczą się w znacznie wyższym przedziale, co obrazuje poniższy histogram:

Podsumowanie

Wyniki interpolacji z wartości godzinowych na interwały 15-minutowe wielkości publikowanych w ramach BPKD funkcjami sklejanymi różnią się w zależności od algorytmu interpolacji. Najlepsze pod względem miary MAPE są zmodyfikowane funkcje sześcienne, ale są dość trudne w implementacji. Nieco gorsze rezultaty dają funkcje sześcienne naturalne – prawdopodobnie z powodu niespełnienia warunku na monotoniczność funkcji pomiędzy węzłami interpolacji. Dość dobre, ale zauważalnie słabsze wyniki daje interpolacja liniowa, jest ona jednak bardzo prosta we wdrożeniu. Interpolacja funkcjami stałymi, w porównaniu do interpolacji sześciennej i liniowej daje już dużo gorsze wyniki, natomiast interpolację funkcjami kwadratowymi należy z góry odrzucić.

Wyniki mogą różnią się także w zależności od interpolowanych wielkości, co jest naturalnym następstwem ich zmienności. W przypadku, gdy występują znaczne wahania w ramach jednej godziny (tak, jak w przypadku dostępnych rezerw mocy), wyniki interpolacji będą znacznie gorsze. Jednak bez względu na rodzaj rozpatrywanych powyżej wielkości, metody sześcienne dały zawsze najlepsze rezultaty.

Podziękowanie

Przy wyznaczaniu wartości interpolowanych skorzystałem z algorytmów zaimplementowanych w bibliotece ACQ (https://github.com/ratesquant/ACQ). Dziękuję serdecznie jej autorom za jej utworzenie i udostępnienie.